Error-handling with classy optics in Scala

Introduction (part 1)

First, we want to more succinctly state the problem. We want to be able to write code so that we can “automatically handle errors” i.e. in the same way the Java keyword throws works, we don’t have to catch and then re-throw, we just say throws up to the handling function, which essentially “case matches” on whether we have an error or a succeeding value. This is akin to the Either[E, ?] monad behaviour.

If we follow this path naively, we will quickly run into another problem. For example:

• def f potentially produces errors E1 or E2
• def g potentially produces errors E3 or E4
• def h calls both f and g and so potentially produces the sum of the errors of f and g

This problem propagates all throughout the function call tree. We have a number of options in this case. Here is one naive solution: modify the types of f and g to potentially produce all of E1, E2, E3 or E4, knowing that two of these conditions will never occur. This means that when reasoning about the code, the type of f is wider than is necessary, and any other caller of f (not h) is going to have to deal with these conditions in some way, whether by propagation, or by throwing an exception.

What we want is the convenience associated with this solution, but without the unsafe code that would otherwise haunt us now, as we try to read and comprehend the code, and in the future when that exception occurs (because it will). This particular problem has a strong relationship to what is known as The Expression Problem (Wadler). Specifically, we want to add constructors to a data type as “more possible errors can occur”, but that means all calling code needs to be modified to handle any new constructor. At the opposite extreme, we open up the data type constructors, so that “adding new constructors” has no effect on the calling code, however, this results in a lack of safety up the call tree (which functions use which values?). This opening of the data type comes in various forms, but can typically be implemented by saying, “errors are all String”, then use each String value to denote the error type. This particular information means that error values cannot carry data, or at least, that data is carried in the String which must be parsed out. Neither of these are desirable.

There is a dual to this problem, which manifests itself in every-day programming in many ways. For example, “the schema update problem”, whereby a database table has a column added, which has an effect on all the calling code. Unlike adding a constructor to a sum type, in this case, we have added a field to a product type. We try to get around this problem with “schema versions” and various other strategies, and I’m sure we’ve all experienced the consequences of these types of strategies.

I am going to introduce an abstraction that works toward resolving both of these problems (and more). This is not to say there are no drawbacks; there are, however, these drawbacks are almost always far more acceptable that those previously referenced.

Before I do, let’s talk about this problem a bit more loosely and intuitively. We first observe that data types are made of constructors or fields, each of which is made up of data types and so on. That is to say, when we talk about a data type, we have a recursive definition in relation to its components: “data types are sums and products of data types”. There are several kinds of relationship between a data type and its components. I will choose four to talk about, as these are a good introduction, relate to our typical programming tasks, and other relationships are then easy to follow.

1. data type A has exactly zero or many B and/or some other things
2. data type A has exactly one B or some other things
3. data type A has exactly one B and some other things
4. data type A has exactly one B and no other things

Let’s discuss these relationships in more detail.

data type A has exactly zero or many B and/or some other things

This is a (relatively) general relationship and so arises often. Here are some examples:

case class A(n: Int, s1: String, s2: String)

It can be said that the data type A has zero or many String values. It actually has two String fields, however, this is just one view of our relationship. We could talk about just one of the String fields, or neither, and we would still be meeting the definition of our relationship. Let’s expression this relationship as follows: A *=> String where we might intuit this in our minds as, “view zero or many String values through A”.

The term view here is used generally; it does not necessitate, “getting the values”, only that we can apply some sort of focus on those String values through the A value.

case class A(n: Int, b: Boolean, s: String, ss: List[String])

Again, we have the relationship, A *=> String.

data type A has exactly one B or some other things

This relationship is often discussed when it comes to sum types. For example, Option[X] has exactly one X or some other things (those other things being Unit). Here is another example:

sealed trait A
case class IsInt(n: Int) extends A
case class IsString(s: String) extends A

The data type A has exactly one Int or some other things. The same relationship can be said for String.

We will express this relationship as A ?=> Int and take it to mean, “we focus on zero or many Int values through a value of the type A”

data type A has exactly one B and some other things

This relationship pertains to product types. For example, Tuple2[X, Y] has exactly one X and some other things (in this case, Y). We might have a record (product) such as:

case class Person(age: Int, name: String)

This relationship applies between a Person and Int i.e. a Person has exactly one Int and some other things. The same is true for String.

We will expression this relationship as Person &=> Int and take it to mean, “we focus on exactly one Int value through a value of the type Person”

data type A has exactly one B and no other things

This relationship is relatively restrictive. It applies when we have a “newtype”. For example:

case class CorrelationId(s: String)

It can be said that CorrelationId has a String and no other things.

We will express this relationship as CorrelationId ==> String and take it to mean, “we focus on exactly one String value through a value of the type CorrelationId”. Incidentally, since there are “no other things”, an inverse arises such that we can “focus on exactly one CorrelationId value through a value of the type String”.

It can also be observed (by implication) that there is a hierarchy in the relationships here. That is, some relationships are specialisations of others. We can express this in a diagram:

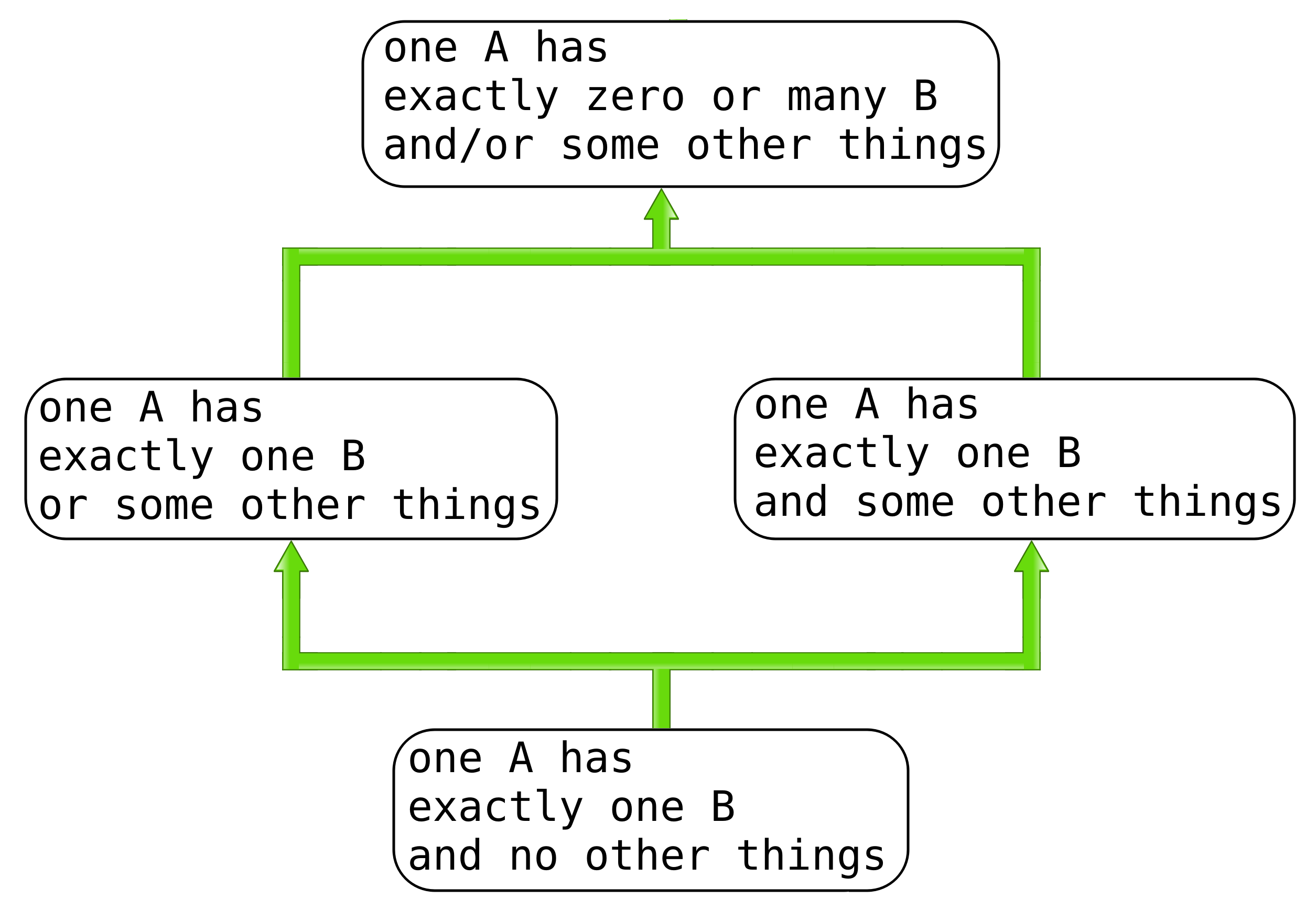
We want to find a generalisation that expresses these relationships (and others that have been omitted) and specialise as necessary.

The first abstraction to talk about is called an Optic. There are other formulations of this abstraction, however, we will use the traditional formulation, because I believe it helps in providing a pedagogical explanation, regardless of any technical trade-offs (note: opinions exist here).

trait Optic[~>[_, _], F[_], A, B] {
  def run: (B ~> F[B]) => A ~> F[A]
}

The Optic abstraction, defined over values A and B, depict a relationship from data type A to B. In its most general form, i.e. an Optic itself, denotes the relationship “A is exactly equal to B”. Note that this relationship is distinct to isomorphism (a slightly weaker relationship).

It may be observed that the Optic#run function looks almost like a modify operation. Consider the following product type and modify operation:

case class Person(age: Int, name: String) 

def modify: (String => String) => Person => Person = k => {
  case Person(a, n) => Person(a, k(n))
}

or similarly, on a sum type:

sealed trait A
case class IsInt(n: Int) extends A
case class IsString(s: String) extends A

def modify: (String => String) => A => A = k => {
  case IsInt(n) => IsInt(n)
  case IsString(s) => IsString(k(s))
}

This observation between modify and the Optic data type is not coincidental. If we specialise Optic[~>[_, _], F[_], A, B] so that the first type parameter is Function1 and we eliminate the second type parameter F with Identity (see below), we have essentially recovered a modify operation from A to B.

case class Identity[A](a: A)

Our four relationships (and others) can be expressed using this Optic abstraction. We can do this by specialising the ~> and F type parameters. That is a story for parts >1.

However, here is some fun practice. First, I will make this claim: given an Optic you can write a pair of get and set functions for the data type relationships. That is to say, these functions are possible to write. However, you will need to specialise ~> and F.

Specifically: * to implement get, specialise ~> to Function1 and F to Const[B, ?] (that B is the same one in the Optic definition) * to implement set, specialise ~> to Function1 and F to Identity

Here are the Identity and Const data types and their Functor implementations:

case class Identity[A](value: A)

case class Const[X, A](value: X)

trait Functor[F[_]] {
  def fmap[A, B](f: A => B): F[A] => F[B]
}

object Functor {
  implicit val IdentityFunctor: Functor[Identity] =
    new Functor[Identity] {
      def fmap[A, B](f: A => B) =
        i =>
          Identity(f(i.value))
    }

  implicit def ConstFunctor[X]: Functor[({type l[A]=Const[X, A]})#l] =
    new Functor[({type l[A]=Const[X, A]})#l] {
      def fmap[A, B](f: A => B) =
        c =>
          Const(c.value)
    }
}

And now it is possible to write get and set from a given Optic:

trait Optic[~>[_, _], F[_], A, B] {
  def run: (B ~> F[B]) => A ~> F[A]
}

object Problem[A, B] {
  def get(optic: Optic[Function1, ({type l[A]=Const[B, A]})#l, A, B]): A => B =
    ???

  def set(optic: Optic[Function1, Identity, A, B]): A => B => A =
    ???
}

Spoiler Alert

The answer follows:

object Problem {
  def get[A, B](optic: Optic[Function1, ({type l[A]=Const[B, A]})#l, A, B]): A => B =
    a =>
      optic.run(b => Const(b))(a).value

  def set[A, B](optic: Optic[Function1, Identity, A, B]): A => B => A =
    a => b =>
      optic.run(_ => Identity(b))(a).value
}

Perhaps more interestingly, we can write implementations of an Optic which satisfy both of these types. We will do this by generalisation. Both Const[X, A] and Identity are instances of Functor and that is all that is required to write an implementation.

object Implementation {
  case class Person(age: Int, name: String)

  def age[F[_]: Functor]: Optic[Function1, F, Person, Int] =
    new Optic[Function1, F, Person, Int] {
      def run =
        k => p => {
          implicitly[Functor[F]].fmap[Int, Person](a => Person(a, p.name))(k(p.age))
        }
    }

  def name[F[_]: Functor]: Optic[Function1, F, Person, String] =
    new Optic[Function1, F, Person, String] {
      def run =
        k => p => {
          implicitly[Functor[F]].fmap[String, Person](n => Person(p.age, n))(k(p.name))
        }
    }

and then use it!

object Main {
  def main(args: Array[String]): Unit = {
    import Problem._

    val fred = Person(45, "Fred")
    val n = get[Person, Int](age)(fred)
    println(n) // 45

    val p1 = set[Person, Int](age)(fred)(46)
    println(p1) // Person(46,Fred)

    val p2 = set[Person, String](name)(p1)("Mary")
    println(p2) // Person(46,Mary)
  }
}